Question

The lengths of pregnancy terms for a particular species of mammal are nearly normally distributed about a mean pregnancy length with a standard deviation of days. About what percentage of births would be expected to occur within days of the mean pregnancy​ length?

About what​% of births would be expected to occur within days of the mean pregnancy length.

Answer 1

Answer: About 99.74% of births would be expected to occur within 24 days of the mean pregnancy length.

Explanation:

Complete question is attached below.

Given: The lengths of pregnancy terms for a particular species of mammal are nearly normally distributed about a mean pregnancy length with a standard deviation of 8 days.

i.e.
`\sigma= 8`

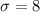
let X denotes the random variable that represents the lengths of pregnancy.

The probability of births would be expected to occur within 24 days of the mean pregnancy​ length:

`P(\mu-24<X<\mu+24)=P((\mu-24-\mu)/(8)<(X-\mu)/(\sigma)<(\mu+24-\mu)/(8))\\\\=P((-24)/(8)<Z<(24)/(8))\ \ \ [\because Z=(X-\mu)/(\sigma)]\\\\=P(-3<Z<3)\\\\=P(Z<3)-P(Z<-3)\\\\=P(Z<3)-(1-P(Z<3))\\\\=2P(Z<3)-1`

`= 2(0.9987)-1\ \ \ [\text{ By z-table}]\\\\=0.9974`

=99.74%

Hence, about 99.74% of births would be expected to occur within 24 days of the mean pregnancy length.