Question

EMERGENCY HELP! A steady stream of water flows into a partially-filled rectangular tank. After 6 minutes, there are 87 gallons of water in the tank. After 21 minutes, there are 222 gallons. Write an equation to represent the volume of water in the tank y after x minutes. How much water was in the tank to begin?

Answer 1

`y=9x+33`

33 gallons of water to begin with.

Explanation:

So, we are essentially given two coordinates: (6,87) and (21,222). To find an equation, we will need to find the slope and y-intercept. We know it's a linear equation because it's a steady stream, meaning a constant slope.

Using the slope formula, the slope is:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)=(222-87)/(21-6)=135/15=9`

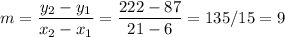
So, the rate at which the stream flows is 9 gallons per minute.

Now, let's find the initial amount of water. To do this, we can use point-slope form. Pick either of the two points. I'm going to use (6,87).

Point-slope form is given by:

`y-y_1=m(x-x_1)`

Substitute:

`y-(87)=9(x-(6))`

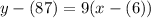
Distribute:

`y-87=9x-54`

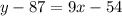
Therefore:

`y=9x+33`

So, there were 33 gallons of water in the tank to begin with.