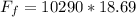Question

For the cellar of a new house, a hole is dug in the ground, with vertical sides going down 2.10 m. A concrete foundation wall is built all the way across the 8.90 m width of the excavation. This foundation wall is 0.189 m away from the front of the cellar hole. During a rainstorm, drainage from the street fills up the space in front of the concrete wall, but not the cellar behind the wall. The water does not soak into the clay soil. Find the force that the water causes on the foundation wall. For comparison, the weight of the water is given by 2.10 m ✕ 8.90 m ✕ 0.189 m ✕ 1000 kg/m3 ✕ 9.80 m/s2 = 34.6 kN.

Answer 1

The force on the foundation wall is
`F_f = 191394 \ N`

Step-by-step explanation:

From the question we are told that

The depth of the hole's vertical side is
`d = 2.10 \ m`

The width of the hole is
`b = 8.90 \ m`

The distance of the concrete wall from the front of the cellar is
`c = 0.189 \ m`

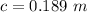
Generally the area which the water from the drainage covers is mathematically represented as

`A = d * b`

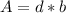
substituting values

`A = 2.10 * 8.90`

`A = 18.69 \ m^2`

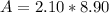
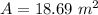
Now the gauge pressure exerted on the foundation wall is mathematically evaluated as

`P_g = \rho * d_(avg) * g`

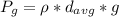
Here is the average height foundation wall where the pressure of the water is felt and it is evaluated as

`d_(avg) = (h_1 + h_2 )/(2)`

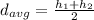
where
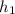`h_1` at the height at bottom of the hole which is equal to
`h_1 = 0`

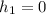
and
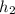`h_2` is the height at the top of the hole
`h_2 = d = 2.10`

`d_(avg) = (0 + 2.10 )/(2)`

`d_(avg) = 1.05`

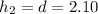
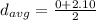
Where
`\rho` is the density of water with constant value
`\rho = 1000 \ kg/m^3`

substituting values

`P_g = 1000 * 1.05 * 9.8`

`P_g = 10290 \ Pa`

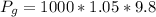
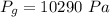
Then the force exerted by the water on the foundation wall mathematically represented as

`F_f = P_g * A`

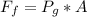
substituting values

`F_f = 10290 * 18.69`

`F_f = 191394 \ N`