Question

g Question 11 pts Consider two masses connected by a string hanging over a pulley. The pulley is a uniform cylinder of mass 3.0 kg. Initially m1 is on the ground and m2 rests 2.9 m above the ground. After the system is released, what is the speed of m2 just before it hits the ground? m1= 30 kg and m2= 35 kg Group of answer choices 2.1 m/s 1.4 m/s 9.8 m/s 4.3 m/s 1.9 m/s

Answer 1

The speed of m2 just before it hits the ground is 2.1 m/s

Step-by-step explanation:

mass on the ground m1 = 30 kg

mass oat rest at the above the ground m2 = 35 kg

height of m2 above the ground =2.9 m

Let the tension on the string be taken as T

for the mass m2 to reach the ground, its force equation is given as

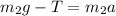`m_(2) g - T = m_(2)a` ....equ 1

where g is acceleration due to gravity = 9.81 m/s^2

and a is the acceleration with which it moves down

For mass m1 to move up, its force equation is

`T - m_(1) g = m_(1) a`

`T = m_(1)a + m_(1)g`

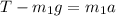
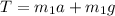
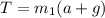`T = m_(1)(a + g)` ....equ 2

substituting T in equ 1, we have

`m_(2) g - m_(1)(a+g) = m_(2)a`

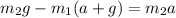
imputing values, we have

`(35*9.81) - 30(a+9.81) = 35a`

`343.35 - 30a-294.3 = 35a`

`343.35 -294.3 = 35a+ 30a`

`49.05 = 65a`

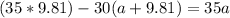
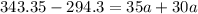
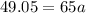
a = 49.05/65 = 0.755 m/s^2

The initial velocity of mass m2 = u = 0

acceleration of mass m2 = a = 0.755 m/s^2

distance to the ground = d = 2.9 m

final velocity = v = ?

using Newton's equation of motion

`v^(2)= u^(2) + 2ad`

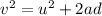
substituting values, we have

`v^(2)= 0^(2) + 2*0.755*2.9`

`v^(2)= 2*0.755*2.9 = 4.379\\v = √(4.379)`

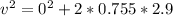
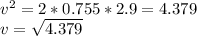
v = 2.1 m/s