Question

A lead ball weighs 326 grams. Find the radius of the ball to the nearest tenth of a

centimeter.

Answer 1

1.9cm

Explanation:

The density d of a material is related to its mass m and volume V as follows;

d =
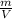`(m)/(V)` ------------------(i)

The material in question here is the lead ball.

Now, from known experiment;

the density of lead is 11.34g/cm³

From the question, the weight/mass of the lead ball is 326g

Substitute these values into equation (i) as follows;

11.34 =
`(326)/(V)`

V =
`(326)/(11.34)`

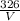
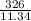
V = 28.75cm³

Now, since the ball is of course spherical, we can get the radius by using the following relation from the volume of a sphere;

V =
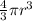`(4)/(3) \pi r^3` [V = volume, r = radius]

V = 28.75cm³

=> 28.75 =
`(4)/(3) \pi r^3`

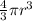
=> 3 x 28.75 = 4 π r³

=> 86.25 = 4 π r³

=> 21.5625 = π r³ [Take π = 3.142]

=> 21.5625 = (3.142) r³ [divide both sides by 3.142]

=> 6.86 = r³ [Take the cube root of both sides]

=> ∛6.86 = ∛r³

=> 1.90 = r

Therefore, the radius is 1.9cm to the nearest tenth