Question

The value of the z-scores in a hypothesis test is influenced by a variety of factors. Assuming that all other variables are held constant, explain how the value of z is influenced by each of the following: (Hint: When coming up with your answer, consider how changing the corresponding value in the z formula would change things if its value was increased by 10, 100, 1000, etc. while all other values constant.)

Increasing the difference between the sample mean and the original population mean will result in a(n) (increase/decrease) ______ in the absolute value of z, and a(n) (increase/decrease) ______ in the probability of obtaining a sample with that mean.
Increasing the population standard deviation will result in a(n) (increase/decrease) _____in the absolute value of z, and a(n) (increase/decrease) ______in the probability of obtaining a sample with that mean.
Increasing the number of scores in the sample will result in a(n) (increase/decrease) _____ in the absolute value of z, and a(n) (increase/decrease)______in the probability of obtaining a sample with that mean.

Answer 1

Explained below.

Explanation:

The z-test statistic is given as follows:

`Z=(\bar X-\mu)/(\sigma/√(n))`

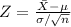
Here,

`\bar X=\text{Sample Mean}\\\\\mu=\text{Population Mean}\\\\\sigma=\text{Population standard deviation}\\\\n=\text{Sample size}`

The p-value is well-defined as per the probability, [under the null-hypothesis (H₀)], of attaining a result equivalent to or greater than what was the truly observed value of the test statistic.

(i)

The difference between the sample mean and the original population mean are directly proportional to the z-test statistic.

So, increasing the difference between
`\bar X` and
`\mu` will lead to an increase in the z-score.

And as the Z-score increases the p-value of the test decreases.

Thus, the complete statement is:

"Increasing the difference between the sample mean and the original population mean will result in an increase in the absolute value of z, and a decrease in the probability of obtaining a sample with that mean."

(ii)

The population standard deviation is inversely proportional to the z-test statistic.

So, increasing the population standard deviation will lead to a decrease in the z-score.

And as the Z-score decreases the p-value of the test increases.

Thus, the complete statement is:

"Increasing the population standard deviation will result in a decrease in the absolute value of z, and an increase in the probability of obtaining a sample with that mean"

(iii)

The number of scores in the sample is directly proportional to the z-test statistic.

So, increasing the number of scores in the sample will lead to an increase in the z-score.

And as the Z-score increases the p-value of the test decreases.

Thus, the complete statement is:

"Increasing the number of scores in the sample will result in an increase in the absolute value of z, and an decrease in the probability of obtaining a sample with that mean."