Answer:
a
The speed of wave is
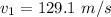
b
The new speed of the two waves is
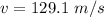
Step-by-step explanation:
From the question we are told that
The mass of the string is
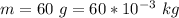
The length is
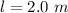
The tension is
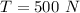
Now the velocity of the first wave is mathematically represented as
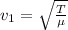
Where
 is the linear density which is mathematically represented as
is the linear density which is mathematically represented as
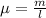
substituting values
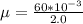
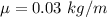
So

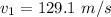
Now given that the Tension, mass and length are constant the velocity of the second wave will same as that of first wave (reference PHYS 1100 )