Answer:
(a) P(none) = 0.0488
(b) P(at least one) = 0.9512
(c) P(at most one) = 0.2186
(d) No, it doesn't appear that the 24% share value is wrong.
Explanation:
We are given that among the TV sets in use, 24% were tuned to Lett3rs.
A pilot survey begins with 11 households have TV sets in use at the time of a Lett3rs broadcast.
Let X = Number of households that are tuned to Lett3rs
The above situation can be represented through binomial distribution;

where, n = number of samples (trials) taken = 11 households
r = number of success
p = probability of success which in our question is % of
households that were tuned to Lett3rs, i.e; 24%
So, X ~ Binom{n = 11, p = 0.24}
(a) The probability that none of the households are tuned to Lett3rs is given by = P(X = 0)
P(X = 0) =
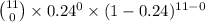
=

= 0.0488
(b) The probability that at least one households are tuned to Lett3rs is given by = P(X
 1)
1)
P(X
 1) = 1 - P(X = 0)
1) = 1 - P(X = 0)
= 1 - 0.0488
= 0.9512
(b) The probability that at most one households are tuned to Lett3rs is given by = P(X
 1)
1)
P(X
 1) = P(X = 0) + P(X = 1)
1) = P(X = 0) + P(X = 1)
=
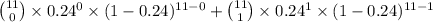
=
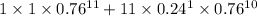
= 0.2186
No, it doesn't appear that the 24% share value is wrong because the probability that at most one household is tuned to Lett3rs is somewhere close to 24% and this probability is also not unusual as it is way more than the criteria of more than 5%.