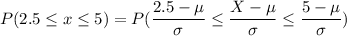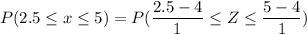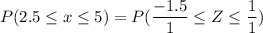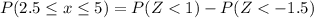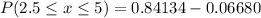Answer:
the probability that a randomly selected college student will take between 2.5 and 5 minutes to find a parking spot in the library lot is 0.77454
Explanation:
Given that:
mean = 4
standard deviation = 1
The objective is to find the probability that a randomly selected college student will take between 2.5 and 5 minutes to find a parking spot in the library lot.
i.e