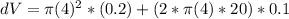Answer:
The volume is

Explanation:
From the question we are told that
The height is h = 20 cm
The diameter is d = 8 cm
The thickness of both top and bottom is dh = 2 * 0.1 = 0.2 m
The thickness of one the side is dr = 0.1 cm
The radius is mathematically represented as
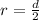
substituting values
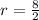
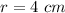
Generally the volume of a cylinder is mathematically represented as
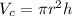
Now the partial differentiation with respect to h is

Now the partial differentiation with respect to r is
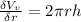
Now the Total differential of
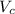 is mathematically represented as
is mathematically represented as
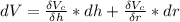
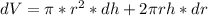
substituting values