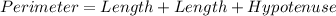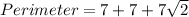Answer:

Explanation:
Given:
Area of the square = 49 in²
Required
Determine the perimeter of the one of the congruent triangles
First, we'll determine the length of the square;
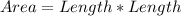
Substitute 49 for Area
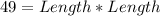
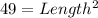
Take Square root of both sides
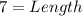
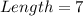
When the square is divided into two equal triangles through the diameter;
2 sides of the square remains and the diagonal of the square forms the hypotenuse of the triangle;
Calculating the diagonal, we have;
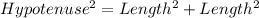 -- Pythagoras Theorem
-- Pythagoras Theorem
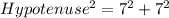
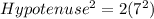
Take square root of both sides
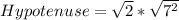
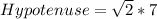

The perimeter of one of the triangles is the sum of the 2 Lengths and the Hypotenuse