Question

Find the indicated probability. Round to the nearest thousandth.

A study conducted at a certain college shows that 55% of the school's graduates find a job in their chosen field within a year after graduation. Find
the probability that among 7 randomly selected graduates, at least one finds a job in his or her chosen field within a year of graduating.
0.985
0.996
0.550
0.143

Answer 1

`P(At\ least\ 1) = 0.985`

Explanation:

Given

Proportion = 55%

Required

Probability that at least one out of 7 selected finds a job

Let the proportion of students that finds job be represented with p

`p = 55\%`

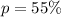
Convert to decimal

`p = 0.55`

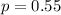
Let the proportion of students that do not find job be represented with q

Such that;

`p + q = 1`

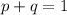
Make q the subject of formula

`q = 1 - p`

`q = 1 - 0.55`

`q = 0.45`

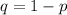
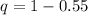
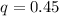
In probability; opposite probabilities add up to 1;

In this case;

Probability of none getting a job + Probability of at least 1 getting a job = 1

Represent Probability of none getting a job with P(none)

Represent Probability of at least 1 getting a job with P(At least 1)

So;

`P(none) + P(At\ least\ 1) = 1`

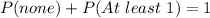
Solving for the probability of none getting a job using binomial expansion

`(p + q)^n = ^nC_0p^nq^0 + ^nC_1p^(n-1)q^1 +.....+^nC_np^0q^n`

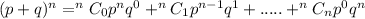
Where
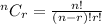`^nC_r = (n!)/((n-r)!r!)` and n = 7; i.e. total number of graduates

For none to get a job, means 0 graduate got a job;

So, we set r to 0 (r = 0)

The probability becomes

`P(none) = ^nC_0p^nq^0`

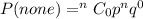
Substitute 7 for n

`P(none) = (7!)/((7-0)!0!) * p^7 * q^0`

`P(none) = (7!)/(7!0!) * p^7 * q^0`

`P(none) = (7!)/(7! * 1) * p^7 * q^0`

`P(none) = 1 * p^7 * q^0`

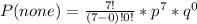
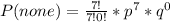
Substitute
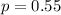`p = 0.55` and
`q = 0.45`

`P(none) = 1 * 0.55^7 * 0,45^0`

`P(none) = 0.01522435234`

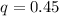
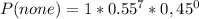
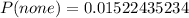
Recall that

`P(none) + P(At\ least\ 1) = 1`

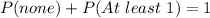
Substitute
`P(none) = 0.01522435234`

`0.01522435234+ P(At\ least\ 1) = 1`

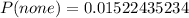
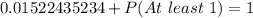
Make P(At least 1) the subject of formula

`P(At\ least\ 1) = 1 - 0.01522435234`

`P(At\ least\ 1) = 0.98477564766`

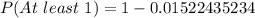
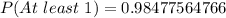
`P(At\ least\ 1) = 0.985` (Approximated)