Question

Find the area and the perimeter of the shaded regions below. Give your answer as a completely simplified exact value in terms of π (no approximations). The figures below are based on semicircles or quarter circles and problems b), c), and d) are involving portions of a square. Need help quick Plz!!!

Answer 1

The answer is below

Explanation:

The shape of the figure attached is the shape of a sector with an angle of 90° (quarter of a circle).

From the sector, AB = AC = radius of the sector (r) = 12. Therefore:

`Area\ of\ sector=(\theta)/(360)*\pi r^2 = (90)/(360)*\pi * (12)^2 = 0.25 * \pi * 144=36\pi\\\\Area\ of\ triangle\ ABC=(1)/(2)*base *height= (1)/(2)*AB*BC=(1)/(2)*12*12=72\\\\Area \of\ shaded\ region = Area\ of\ sector-Area\ of\ triangle=36\pi-72\\\\Area \of\ shaded\ region =36\pi-72`

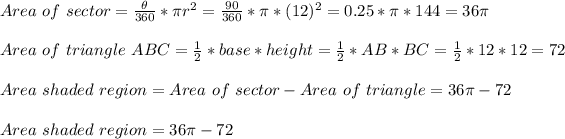
From the triangle: AC² = AB² + BC²

AC² = 12² + 12² = 144 + 144

AC² = 288

AC=√288 = 12√2

`Perimeter\ of\ sector=(\theta)/(360)*2\pi r = (90)/(360)*2\pi * (12) = 0.25 * 2\pi * 12=6\pi\\\\Perimeter \of\ shaded\ region = Perimeter\ of\ sector+AC=6\pi + 12√(2)`