Question

A circular loop of wire has radius of 9.50 cm. A sinusoidal electromagnetic plane wave traveling in air passes through the loop, with the direction of the magnetic field of the wave perpendicular to the plane of the loop. The intensity of the wave at the location of the loop is 0.0295 W/m^2, and the wavelength of the wave is 6.40 m.

Required:
What is the maximum emf induced in the loop?

Answer 1

The maximum emf induced in the loop is 0.132 Volts

Step-by-step explanation:

Given;

radius of the circular loop, r = 9.5 cm

intensity of the wave, I = 0.0295 W/m²

wavelength, λ = 6.40 m

The intensity of the wave is given as;

`I = (B_o^2*c )/(2\mu_o)`

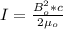
where;

B₀ is the amplitude of the field

c is the speed of light = 3 x 10⁸ m/s

μ₀ is permeability of free space = 4π x 10⁻⁵ m/A

`I = (B_o^2*c )/(2\mu_o)\\\\B_o^2 = (I*2\mu_o)/(c) \\\\B_o^2 = (0.0295*2*4\pi*10^(-7))/(3*10^8) \\\\B_o^2 = 2.472 *10^(-16)\\\\B_o = \sqrt{2.472 *10^(-16)}\\\\ B_o = 1.572*10^(-8) \ T`

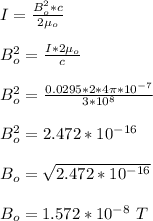
Area of the circular loop;

A = πr²

A = π(0.095)²

A = 0.0284 m²

Frequency of the wave;

f = c / λ

f = (3 x 10⁸) / (6.4)

f = 46875000 Hz

Angular velocity of the wave;

ω = 2πf

ω = 2π(46875000)

ω = 294562500 rad/s

The maximum induced emf is calculated as;

emf = B₀Aω

= (1.572 x 10⁻⁸)(0.0284)(294562500)

= 0.132 Volts

Therefore, the maximum emf induced in the loop is 0.132 Volts