Answer:
The probability is
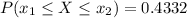
Explanation:
From the question we are told that
The population mean is
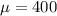
The standard deviation is
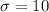
The considered values are
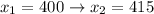
Given that the weight follows a normal distribution
i.e

Now the probability of a weight between 415 pounds and the mean of 400 pounds is mathematically as

So
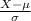 is equal to Z (the standardized value of X )
is equal to Z (the standardized value of X )
Hence we have

substituting values
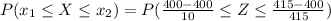
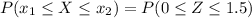

From the standardized normal distribution table
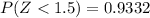 and
and
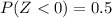
So
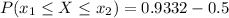
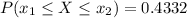
NOTE : This above values obtained from the standardized normal distribution table can also be obtained using the P(Z) calculator at (calculator dot net).