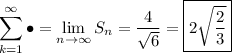Question

For the following telescoping​ series, find a formula for the nth term of the sequence of partial sums ​{Sn​}. Then evaluate Lim Sn to obtain the value of the series or state that the series diverges.

n→[infinity]
[infinity]
Σ (4/√k+5 ) - 4/ √ k+6)
k=1

Answer 1

Looks like the series is

`\displaystyle\sum_(k=1)^\infty\left(\frac4{√(k+5)}-\frac4{√(k+6)}\right)`

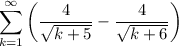
This series has n-th partial sum

`S_n=\displaystyle\sum_(k=1)^n\bullet`

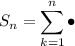
(where
`\bullet` is used as a placeholder for the summand)

`S_n=\displaystyle\left(\frac4{\sqrt6}-\frac4{\sqrt7}\right)+\left(\frac4{\sqrt7}-\frac4{\sqrt8}\right)+\cdots+\left(\frac4{√(n+4)}-\frac4{√(n+5)}\right)+\left(\frac4{√(n+5)}-\frac4{√(n+6)}\right)`

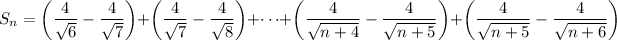
In each grouped term, the last term is annihilated by the first term of the next group; that is, for instance,

`\displaystyle\left(\frac4{\sqrt6}-\frac4{\sqrt7}\right)+\left(\frac4{\sqrt7}-\frac4{\sqrt8}\right)=\frac4{\sqrt6}-\frac4{\sqrt8}`

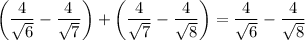
Ultimately, all the middle terms will vanish and we're left with

`S_n=\frac4{\sqrt6}-\frac4{√(n+6)}`

As
`n\to\infty`, the last term converges to 0 and we're left with

`\displaystyle\sum_(k=1)^\infty\bullet=\lim_(n\to\infty)S_n=\frac4{\sqrt6}=\boxed{2√(\frac23)}`