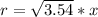Answer:

Step-by-step explanation:
The options are not well presented; However, the solution is as follows
Given
Shape: Cone

Height = x
Required
Find the radius of the cone
The volume of a cone is:
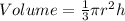
Where h represents height and r represents radius;
Substitute x for h and
 for Volume
for Volume

Multiply both sides by 3
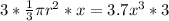
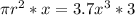
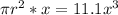
Multiply both sides by x
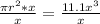
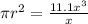

Take π as 3.14
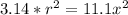
Divide both sides by 3.14
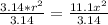
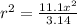
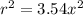
Take Square root of both sides
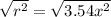
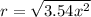
Split the square root