Question

Please answer it now in two minutes

Answer 1

901.1 km²

Explanation:

The area of ∆WXY can be found using the formula, ½*a*b*sin(θ),

Where a and b, are two known sides of the triangle, and θ is the angle between both sides.

To find the area of ∆WXY, follow the steps below:

Step 1: Find XY using the law of sines.

m < W = 180 - (65 + 48) (sum of angles in a ∆)

W = 180 - (113) = 67°

X = 65°

WY = 49 km

XY = ?

`(XY)/(sin(W)) = (WY)/(sin(X))`

`(XY)/(sin(67)) = (49)/(sin(65))`

`(XY)/(0.92) = (49)/(0.91)`

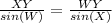
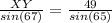
Cross multiply

`XY*0.91 = 49*0.92`

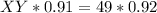
Divide both sides by 0.91

`(XY*0.91)/(0.91) = (49*0.92)/(0.91)`

`XY = 49.54`

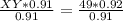
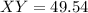
XY ≈ 49.5

Step 2: find the area

Area = ½*WY*XY*sin(Y)

Area = ½*49*49.5*sin(48)

Area = ½*49*49.5*0.743

Area = 901.07325

Area = 901.1 km² (nearest tenth)