Question

A gas of unknown identity diffuses at a rate of 155 mL/s in a diffusion apparatus in which carbon dioxide diffuses at the rate of 102 mL/s. Calculate the molecular mass of the unknown gas.

Answer 1

19.07 g mol^-1

Step-by-step explanation:

The computation of the molecular mass of the unknown gas is shown below:

As we know that

`(Diffusion\ rate\ of unknown\ gas )/(CO_(2)\ diffusion\ rate) = \frac{\sqrt{CO_(2\ molar\ mass)} }{√(Unknown\ gas\ molercular\ mass ) }`

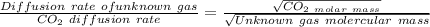
where,

Diffusion rate of unknown gas = 155 mL/s

CO_2 diffusion rate = 102 mL/s

CO_2 molar mass = 44 g mol^-1

Unknown gas molercualr mass = M_unknown

Now placing these values to the above formula

`(155mL/s)/(102mL/s) = \frac{\sqrt{44 g mol^(-1)} }{\sqrt{M_(unknown)} } \\\\ 1.519 = \frac{\sqrt{44 g mol^(-1)} }{\sqrt{M_(unknown)} } \\\\ {\sqrt{M_(unknown)} } = \frac{\sqrt{44 g mol^(-1)}}{1.519} \\\\ {\sqrt{M_(unknown)} } = (44 g mol^(-1))/((1.519)^(2))`

After solving this, the molecular mass of the unknown gas is

= 19.07 g mol^-1