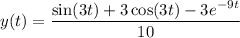Question

Solve the given integral equation for LaTeX: y(t)y ( t ). LaTeX: y(t)+9\displaystyle{\int_{0}^{t}e^{9(t-v)}y(v)\, dv}=\sin(3t)y ( t ) + 9 ∫ 0 t e 9 ( t − v ) y ( v ) d v = sin ⁡ ( 3 t ) Group of answer choices LaTeX: y(t)=3\cos(3t)+9\sin(3t)-9 y ( t ) = 3 cos ⁡ ( 3 t ) + 9 sin ⁡ ( 3 t ) − 9 LaTeX: y(t)=3\cos(3t)+\sin(3t)-3 y ( t ) = 3 cos ⁡ ( 3 t ) + sin ⁡ ( 3 t ) − 3 LaTeX: y(t)=3\cos(3t)+\sin(3t) y ( t ) = 3 cos ⁡ ( 3 t ) + sin ⁡ ( 3 t ) LaTeX: y(t)=3\cos(3t)+9\sin(3t) y ( t ) = 3 cos ⁡ ( 3 t ) + 9 sin ⁡ ( 3 t ) LaTeX: y(t)=\cos(3t)+3\sin(3t)-3

Answer 1

Looks like the equation is

`y(t)+9\displaystyle\int_0^te^(9(t-v))y(v)\,\mathrm dv=\sin(3t)`

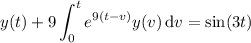
Differentiating both sides yields the linear ODE,

`y'(t)+9e^(9(t-t))y(t)=3\cos(3t)`

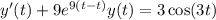
or

`y'(t)+9y(t)=3\cos(3t)`

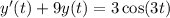
Multiply both sides by the integrating factor
`e^(9t)`:

`e^(9t)y'(t)+9e^(9t)y(t)=3e^(9t)\cos(3t)`

`\left(e^(9t)y(t)\right)'=3e^(9t)\cos(3t)`

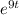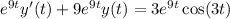
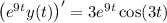
Integrate both sides, then solve for
`y(t)`:

`e^(9t)y(t)=\frac1{10}e^(9t)(\sin(3t)+3\cos(3t))+C`

`y(t)=(\sin(3t)+3\cos(3t))/(10)+Ce^(-9t)`

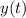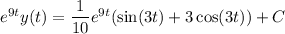
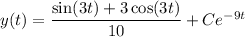
The given answer choices all seem to be missing C, so I suspect you left out an initial condition. But we can find one; let
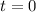`t=0`, then the integral vanishes and we're left with
`y(0)=0`. So

`0=(0+3)/(10)+C\implies C=-\frac3{10}`

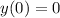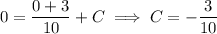
So the particular solution is

`y(t)=(\sin(3t)+3\cos(3t)-3e^(-9t))/(10)`