Answer:
a. True
b. False
c. True
d. False
Explanation:
a. Meaning
as we can see that x is an element of Y
So notation is
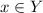
Therefore x is the subset of Y if each of an element of X is also an element of Y.
So notation is

2. (a) We need to proof
When

We will say that A, B and C are the set that is
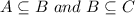
When A = ∅ then
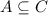 which shows true, as the set of empty is a subset of each set.
which shows true, as the set of empty is a subset of each set.
Hence, it is safe to say that A is not the empty set.
Now we will proof directly
Let us say x be an element of A
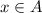
As
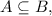 each of the element of A is also an element of B
each of the element of A is also an element of B
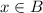
As
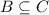 , each if the element of B is also an element of C
, each if the element of B is also an element of C
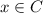
Therefore, as we can see that each of an element of A is also known an element of C, that states
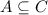
So, the given statement is true, as we conclude with a proof.
(b). We will assume {1}, B = {{1},2} and C = {{1},2,3}
As in the point a, which is an element of B, that is
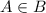 which is true
which is true
As all of the elements in B are also an element in C,
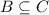 which is also correct.
which is also correct.
Although,
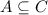 is false as 1 is an element of A that is not in C.
is false as 1 is an element of A that is not in C.
(c) We need to proof
When
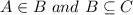 then
then

Let us assume that A, B and C are the sets that
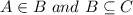
As,
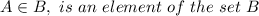
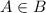
As,
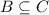 , each of the element of B is also an element of C
, each of the element of B is also an element of C
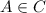
So, its true.
(d) We will assume {1}, B = {{1},2} and C = {{1},2,3}
As in the point a, which is an element of B, that is
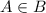 which is true
which is true
As {{1},2} is an element of B,
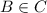 is correct
is correct
Although
 is not correct as {1) is not an element in C.
is not correct as {1) is not an element in C.
SO the statement is false