Question

Given trapezoid PQRS, find the length of midsegment TU.

Answer 1

Option (4)

Explanation:

In the given picture,

Trapezoid PQRS has two points T and U as the midpoints of sides PS and RQ.

Segment TU joins the midpoints of the sides PS and RQ.

Mid-segment theorem states that "If a line joining midpoints of a trapezoid is parallel to the bases, length of this segment is half the sum of lengths of the bases."

Therefore, m(TU) =
`(1)/(2)(m\text{PQ}+m\text{SR})`

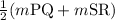
7x - 26 =
`(1)/(2)[(3x+23)+(9x-3)]`

7x - 26 = 6x + 10

7x - 6x = 26 + 10

x = 36

m(TU) = 7x - 26

= 7(36) - 26

= 252 - 26

= 226

Therefore, Option (4) will be the answer.