Question

A study is done to see if the average age a "child" moves permanently out of his parents' home in the United States is at most 23. 43 U.S. Adults were surveyed. The sample average age was 24.2 with a standard deviation of 3.7. The p-value is

Answer 1

The p-value is 2.1%.

Explanation:

We are given that a study is done to see if the average age a "child" moves permanently out of his parents' home in the United States is at most 23. 43 U.S. Adults were surveyed.

The sample average age was 24.2 with a standard deviation of 3.7.

Let
`\mu` = true average age a "child" moves permanently out of his parents' home in the United States.

So, Null Hypothesis,
`H_0` :
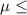`\mu \leq` 23 {means that the average age a "child" moves permanently out of his parents' home in the United States is at most 23}

Alternate Hypothesis,
`H_A` :
`\mu` > 23 {means that the average age a "child" moves permanently out of his parents' home in the United States is greater than 23}

The test statistics that will be used here is One-sample t-test statistics because we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample average age = 24.2

s = sample standard deviation =3.7

n = sample of U.S. Adults = 43

So, the test statistics =
`(24.2-23)/((3.7)/(√(43) ) )` ~
`t_4_2`

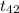
= 2.127

The value of t-test statistics is 2.127.

Now, the p-value of the test statistics is given by;

P-value = P(
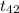`t_4_2` > 2.127) = 0.021 or 2.1%