Question

Construct a 99% confidthence interval for the population mean .Assume the population has a normal distribution. A group of 19 randomly selected employees has a mean age of 22.4 years with a standard deviation of 3.8 years. Round to the nearest tenth.

A) Determine the critical value ta/2 with n-the 1 degrees of freedom
B) Determine the lower and upper bound of the confidence interval
C) Interpret the confidence interval.

Answer 1

Answer with explanation:

Confidence interval for mean, when population standard deviation is unknown:

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))`

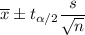
, where
`\overline{x}` = sample mean

n= sample size

s= sample standard deviation

`t_(\alpha/2)` = Critical t-value for n-1 degrees of freedom

We assume the population has a normal distribution.

Given, n= 19 , s= 3.8 ,
`\overline{x}=22.4`

`\alpha=1-0.99=0.01`

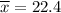
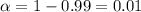
A) Critical t value for
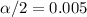`\alpha/2=0.005` and degree of 18 freedom

`t_(\alpha/2)` = 2.8784

B) Required confidence interval:

`22.4\pm ( 2.8744)(3.8)/(√(19))\\\\=22.4\pm2.5058\\\\=(22.4-2.5058,\ 22.4+2.5058)=(19.8942,\ 24.9058)\approx(19.9,\ 24.9)`

Lower bound = 19.9 years

Uppen bound = 24.9 years

C) Interpretation: We are 99% confident that the true population mean of lies in (19.9, 24.9) .