Answer:
a)
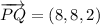 or
or
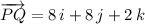 , b) The magnitude of segment PQ is approximately 11.489, c) The two unit vectors associated to PQ are, respectively:
, b) The magnitude of segment PQ is approximately 11.489, c) The two unit vectors associated to PQ are, respectively:
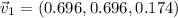 and
and

Explanation:
a) The vectorial form of segment PQ is determined as follows:
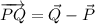
Where
 and
and
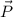 are the respective locations of points Q and P with respect to origin. If
are the respective locations of points Q and P with respect to origin. If
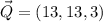 and
and
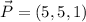 , then:
, then:
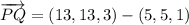
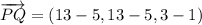
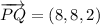
Another form of the previous solution is
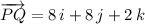 .
.
b) The magnitude of the segment PQ is determined with the help of Pythagorean Theorem in terms of rectangular components:
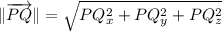
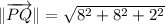
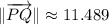
The magnitude of segment PQ is approximately 11.489.
c) There are two unit vectors associated to PQ, one parallel and another antiparallel. That is:
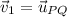 (parallel) and
(parallel) and
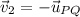 (antiparallel)
(antiparallel)
The unit vector is defined by the following equation:
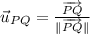
Given that
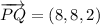 and
and
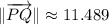 , the unit vector is:
, the unit vector is:
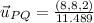
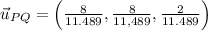
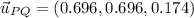
The two unit vectors associated to PQ are, respectively:
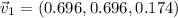 and
and
