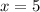Question

How do you solve this type of problem, what would be the procedure? Assume PQRS is a parallelogram, if PQ=x2−10 and SR=3x , find all possible values of x.

Answer 1

`x = 5`

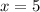
Explanation:

Given

Shape: Parallelogram PQRS

`PQ = x^2 - 10`

`SR = 3x`

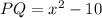
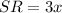
Required

Find all possible values of x

Every parallelogram have parallel and equal opposite sides;

From the given parameters, one can easily deduce that PQ and SR are opposite sides;

This implies that

`PQ = SR`

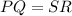
Substitute values of PQ and SR

`x^2 - 10 = 3x`

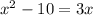
Subtract 3x from both sides

`x^2 - 10 -3x = 3x - 3x`

`x^2 - 10 -3x = 0`

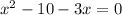
Rearrange

`x^2 -3x- 10 = 0`

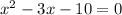
Now, we have a quadratic equation;

Expand the above expression

`x^2 +2x-5x- 10 = 0`

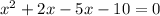
Factorize

`x(x+2)-5(x+2) = 0`

`(x-5)(x+2) = 0`

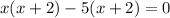
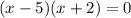
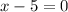`x - 5 = 0` or
`x + 2 = 0`

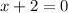
Solve for x in both cases

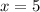`x = 5` or
`x = -2`

But x can't be negative;

So, the possible value of x is

`x = 5`