Question

According to a study conducted by the Gallup Organization, the the proportion of Americans who are afraid to fly is 0.10. A random sample of 1100 Americans results in 121 {0.11} indicating that they are afraid to fly. What is the probability that the sample proportion is more than 0.11

Answer 1

Answer: 0.1457

Explanation:

Let p be the population proportion.

Given: The proportion of Americans who are afraid to fly is 0.10.

i.e. p= 0.10

Sample size : n= 1100

Sample proportion of Americans who are afraid to fly =
`\hat{p}=(121)/(1100)=0.11`

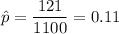
We assume that the population is normally distributed

Now, the probability that the sample proportion is more than 0.11:

`P(\hat{p}>0.11)=P(\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}>\frac{0.11-0.10}{\sqrt{(0.10(0.90))/(1100)}})\\\\=P(z>(0.01)/(0.0090453))\ \ \ [\because z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}} ]\\\\=P(z>1.1055)\\\\=1-P(z\leq1.055)\\\\=1-0.8543=0.1457\ \ \ [\text{using z-table}]`

Hence, the probability that the sample proportion is more than 0.11 = 0.1457