Question

Andrew is about to leave for school. If he walks at a speed of 50 meters per minute, he will arrive 3 minutes after the bell rings. If he runs at a speed of 80 meters per minute, he will arrive 3 minutes before the bell rings. In how many minutes will the bell ring?

Answer 1

The answer is: 13 minutes

Explanation:

First Let us form equations with the statements in the two scenario

`time=(distance)/(speed)`

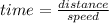
Let the time in which the bell rings be 'x'

1. If Andrew walks (50 meters/minute), he arrives 3 minutes after the bell rings. Therefore the time of arrival at this speed = (3 + x) minutes

`3 + x =(distance)/(50)\\distance = 50(3+x) - - - - - (1)`

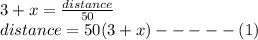
2. If Andrew runs (80 meters/minute), he arrives 3 minutes before the bell rings. Therefore the time taken to travel the distance = (x - 3) minutes

`x - 3 = (distance)/(80) \\distance = 80(x-3) - - - - - (2)`

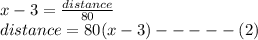
In both cases, the same distance is travelled, therefore, equation (1) = equation (2)

`50(3+x)=80(x-3)`

`150 +50x=80x-240\\`

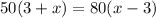
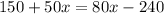
Next, collecting like terms:

`150 + 240 = 80x - 50x\\390 = 30x\\30x = 390\\`

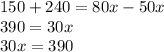
dividing both sides by 3:

x = 390÷30 = 13

∴ x = 13 minutes