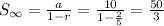Question

Type the correct answer in each box. If necessary, use / for the fraction bar. Complete the statements about series A and B. Series A: 10+4+8/5+16/25+32/125+⋯ Series B: 15+3/5+9/5+27/5+81/5+⋯ Series__ has an r value of___where 0<|r|<1. So, we can find the sum of the series. The sum of the series is___ need help guys please :/

Answer 1

Series A has an r value of 2/5 and series A has an r value of 3. The sum of the series A is 50/3

Explanation:

A geometric sequence is in the form a, ar, ar², ar³, . . .

Where a is the first term and r is the common ratio =
`(a_(n+1))/(a_n)`

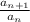
For series A: 10+4+8/5+16/25+32/125+⋯ The common ratio r is given as:

`r=(a_(n+1))/(a_n)=(4)/(10) =(2)/(5)`

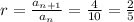
For series B: 1/5+3/5+9/5+27/5+81/5+⋯ The common ratio r is given as:

`r=(a_(n+1))/(a_n)=(3/5)/(1/5) =3`

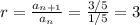
For series A a = 10, r = 2/5, which mean 0 < r < 1, the sum of the series is given as:

`S_(\infty)=(a)/(1-r)=(10)/(1-(2)/(5) ) =(50)/(3)`