Question

a) How many three-digit numbers can be formed from the digits 0, 1, 2, 3, 4, 5, and 6?6x7x7=294 b) How many three-digit numbers can be formed from the digits 0, 1, 2, 3, 4, 5, and 6 if each digit can be used only once?6x6x5=180 c) How many odd numbers can be formed from the digits 0, 1, 2, 3, 4, 5, and 6 if each digit can be used only once?3x5x5=75 d) How many three-digit numbers greater than 330 can be formed from the digits 0, 1, 2, 3, 4, 5, and 6?3x7x7=147/1x3x7=21/147+27=168 e) How many three-digit numbers greater than 330 can be formed from the digits 0, 1, 2, 3, 4, 5, and 6 if each digit can be used only once?1x3x5=15/3x6x5=90/90+15=105

Answer 1

a) 294

b) 180

c) 75

d) 168

e) 105

Explanation:

Given the numbers 0, 1, 2, 3, 4, 5 and 6.

Part A)

How many 3 digit numbers can be formed ?

Solution:

Here we have 3 spaces for the digits.

Unit's place, ten's place and hundred's place.

For unit's place, any of the numbers can be used i.e. 7 options.

For ten's place, any of the numbers can be used i.e. 7 options.

For hundred's place, 0 can not be used (because if 0 is used here, the number will become 2 digit) i.e. 6 options.

Total number of ways =
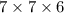`7 * 7 * 6` = 294

Part B:

How many 3 digit numbers can be formed if repetition not allowed?

Solution:

Here we have 3 spaces for the digits.

Unit's place, ten's place and hundred's place.

For hundred's place, 0 can not be used (because if 0 is used here, the number will become 2 digit) i.e. 6 options.

Now, one digit used, So For unit's place, any of the numbers can be used i.e. 6 options.

Now, 2 digits used, so For ten's place, any of the numbers can be used i.e. 5 options.

Total number of ways =
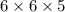`6 * 6 * 5` = 180

Part C)

How many odd numbers if each digit used only once ?

Solution:

For a number to be odd, the last digit must be odd i.e. unit's place can have only one of the digits from 1, 3 and 5.

Number of options for unit's place = 3

Now, one digit used and 0 can not be at hundred's place So For hundred's place, any of the numbers can be used i.e. 5 options.

Now, 2 digits used, so For ten's place, any of the numbers can be used i.e. 5 options.

Total number of ways =
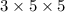`3 * 5 * 5` = 75

Part d)

How many numbers greater than 330 ?

Case 1: 4, 5 or 6 at hundred's place

Number of options for hundred's place = 3

Number of options for ten's place = 7

Number of options for unit's place = 7

Total number of ways =
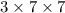`3 * 7 * 7` = 147

Case 2: 3 at hundred's place

Number of options for hundred's place = 1

Number of options for ten's place = 3 (4, 5, 6)

Number of options for unit's place = 7

Total number of ways =
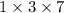`1 * 3 * 7` = 21

Total number of required ways = 147 + 21 = 168

Part e)

Case 1: 4, 5 or 6 at hundred's place

Number of options for hundred's place = 3

Number of options for ten's place = 6

Number of options for unit's place = 5

Total number of ways =
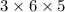`3 * 6 * 5` = 90

Case 2: 3 at hundred's place

Number of options for hundred's place = 1

Number of options for ten's place = 3 (4, 5, 6)

Number of options for unit's place = 5

Total number of ways =
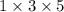`1 * 3 * 5` = 15

Total number of required ways = 90 + 15 = 105