Question

Please help me out with these questions. Its trigonometry.

Find the value of the lettered angles
In case the pic's not clear;

`\cos \alpha = \sin(50 + \alpha )`
​

Answer 1

Answer: i) θ = 30°, 60°, 210°, & 240°

ii) θ = 20° & 200°

Explanation:

i) sin (2θ) = cos 30°

`\sin(2\theta)=(\sqrt3)/(2)\\\\.\quad 2\theta=\sin^(-1)\bigg((\sqrt3)/(2)\bigg)\\\\.\quad 2\theta=60^o\qquad 2\theta=120^o\\\\.\quad \theta=30^o\qquad \theta=60^o`

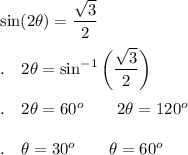
To include all of the solutions for one rotation, add 360/2 = 180 to the solutions above. θ = 30°, 60°, 210°, 240°

If you need ALL of the solutions (more than one rotation), add 180n to the solutions. θ = 30° + 180n & 60° + 180n

*********************************************************************************************

ii) cos α = sin (50 + α)

Use the Identity: cos α = sin (90 - α)

Use Transitive Property to get: sin (50° + α) = sin (90° - α)

50° + α = 90° - α

50° + 2α = 90°

2α = 40°

α = 20°

To find all solutions for one rotation, add 360/2 = 180 to the solution above.

α = 20°, 200°

If you need ALL of the solutions (more than one rotation), add 180n to the solution. α = 20° + 180n