Answer:
The sum is 66
Explanation:
There are a couple formulas to remember.
aₙ = a₁ + d(n-1)
Sₙ =
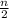 · (a₁ + aₙ)
· (a₁ + aₙ)
In your case "d" equals 4 and a₁ equals 1, that's how we know what the sequence will progress.
Let's plug in the values for the first equation:
aₙ = 1 + 4 (n-1)
Next we can simplify:
aₙ = 1 + 4n-4
aₙ = 4n - 3
Now we can plug in the value for "n" which is 6 for this particular problem:
a₆ = 4 · 6 - 3
a₆ = 21
We can now use the second equation to find the sum:
S₆ =
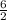 · (1 + 21)
· (1 + 21)
S₆ = 66
Hope this helps =)