Question

A car is being driven, in a straight line and at a uniform speed, towards the base of a vertical tower. The top of the tower is observed from the car and, in the process, it takes 10 min for the angle of elevation to change from 45° to 60°. After how much more time will this car reach the base of the tower? Options: a. 5( √3+ 1 ) b. 6 (√3 +√2) c. 7 (√3- 1) d. 8 (√3-2)

Answer 1

The correct answer is option a.

a. 5( √3+ 1 )

Explanation:

Given that the angle changes from 45° to 60° in 10 minutes.

This situation can be represented as right angled triangles
`\triangle`ABC (in the starting when angle is 45°)and
`\triangle`ABD (after 10 minutes when the angle is 60°).

AB is the tower (A be its top and B be its base).

Now, we need to find the time to be taken to cover the distance D to B.

First of all, let us consider
`\triangle`ABC.

Using tangent property:

`tan\theta =(Perpendicular)/(Base)\\\Rightarrow tan 45=(AB)/(BC)\\\Rightarrow 1=(h)/(BC)\\\Rightarrow h = BC`

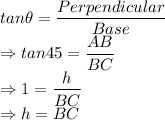
Using tangent property in
`\triangle`ABD:

`\Rightarrow tan 60=(AB)/(BD)\\\Rightarrow \sqrt3=(h)/(BD)\\\Rightarrow BD = (h)/( \sqrt3)\ units`

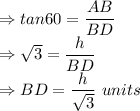
Now distance traveled in 10 minutes, CD = BC - BD

`\Rightarrow h - (h)/(\sqrt3)\\\Rightarrow ((\sqrt3-1)h)/(\sqrt3)`

`Speed =(Distance )/(Time)`

`\Rightarrow ((\sqrt3-1)h)/(10\sqrt3)`

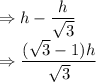
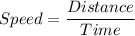
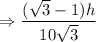
Now, we can say that more distance to be traveled to reach the base of tower is BD i.e. '
`\bold{(h)/(\sqrt3)}`'

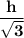So, more time required = Distance left divided by Speed

`\Rightarrow ((h)/(\sqrt3))/(((\sqrt3-1)h)/(10\sqrt3))\\\Rightarrow (h* 10\sqrt3)/(\sqrt3(\sqrt3-1)h)\\\Rightarrow (10 (\sqrt3+1))/((\sqrt3-1)(\sqrt3+1)) (\text{Rationalizing the denominator})\\\Rightarrow (10 (\sqrt3+1))/(3-1)\\\Rightarrow (10 (\sqrt3+1))/(2)\\\Rightarrow 5(\sqrt3+1)}`

So, The correct answer is option a.

a. 5( √3+ 1 )