Question

Select the correct answer.

What is the solution for x in the equation?
25
-- + = 22
-
O A.
T =
-
1+
OB.
=
+10 +
OC.
+
OD.
=

Answer 1

x = 4/3

Explanation:

move (combine) your X's on one side

combine like terms

divide and multiply

Answer 2

`x = (4)/(3)`

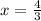
Option B is the correct option.

Explanation:

`- x + (3)/(7) = 2x - (25)/(7)`

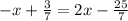
Move variable to L.H.S and change its sign

Similarly, Move constant to R.H.S and change its sign

`- x - 2x = - (25)/(7) - (3)/(7)`

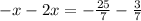
Collect like terms

`- 3x = - (25)/(7) - (3)/(7)`

Calculate the difference

`- 3x = - 4`

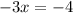
Divide both sides of the equation by -3

`( - 3x)/( - 3) = ( - 4)/( - 3)`

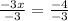
Calculate

`x = (4)/(3)`

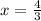
Hope this helps..

Best regards!