Question

Please answer it now in two minutes

Answer 1

Area of the triangle WXY = 365.3 mm²

Explanation:

By applying Sine rule in the given triangle XYW,

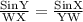
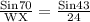
`\frac{\text{SinY}}{\text{WX}}=\frac{\text{SinX}}{\text{YW}}`

`\frac{\text{Sin70}}{\text{WX}}=\frac{\text{Sin43}}{\text{24}}`

WX =
`\frac{24.\text{Sin70}}{\text{Sin43}}`

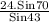
= 33.068 mm

= 33.07 mm

Area of a triangle =
`(1)/(2)a.b.\text{Sin}\theta`

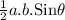
where a and b are the sides of the triangle and θ is the angle between the sides a and b.

Area =
`(1)/(2)(33.07)(24)\text{SinW}`

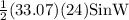
Since, m∠X + m∠Y + m∠W = 180°

m∠W = 180 - (43 + 70)

= 67°

Area of the triangle WXY =
`12* (33.07)\text{Sin67}`

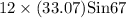
= 365.29 mm²

≈ 365.3mm²