Question

An expression is shown below: 2x3y + 18xy − 10x2y − 90y Part A: Rewrite the expression by factoring out the greatest common factor. Part B: Factor the entire expression completely. Show the steps of your work.

Answer 1

Part A : 2y( x³ + 9x - 5x² - 45 ), Part B : 2y( x - 5 )( x² + 9 )

Explanation:

Part A : Let's break every term down here to their " prime factors ", and see what is common among them,

2x³y + 18xy − 10x²y − 90y -

2x³y = 2
`*` x³
`*` y,

18xy = 2
`*` 3
`*` 3
`*` x
`*` y,

− 10x²y = 2
`*` - 5
`*` x²
`*` y, - so as you can see for this example I purposely broke down - 10 into 2 and - 5. I could have placed the negative on the 2, but as that value was must likely common among all the terms, I decided to place it on the 5. The same goes for " − 90y. " I placed the negative there on the 5 once more.

− 90y = 2
`*` - 5
`*` 3
`*` 3
`*` y

The terms common among each term are 2 and y. Therefore, the GCF ( greatest common factor ) is 2x. Let's now factor the expression using this value.

2y( x³ + 9x - 5x² - 45 )

Part B : Let's simply factor this entire expression. Of course starting with the " factored " expression : 2y( x³ + 9x - 5x² - 45 ),

`2y\left(x^3+9x-5x^2-45\right)` - Factor out "
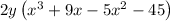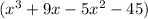`(x^3+9x-5x^2-45\right))` " by grouping,

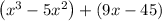`\left(x^3-5x^2\right)+\left(9x-45\right)` - Factor 9 from 9x - 45 and x² from x³ - 5x²,

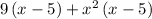`9\left(x-5\right)+x^2\left(x-5\right)` - Factor out common term x - 5,

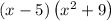`\left(x-5\right)\left(x^2+9\right)` - And our solution is thus 2y( x - 5 )( x² + 9 )