Question

The image of a parabolic lens is traced onto a graph. The function f(x) = (x + 8)(x – 4) represents the image. At which points does the image cross the x-axis?

Answer 1

`\large \boxed{\sf \ \ \ (-8,0) \ \text{ and } \ (4,0) \ \ \ }`

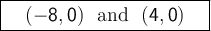
Explanation:

Hello,

from the expression of f(x) we can say that there are two zeroes, -8 with a multiplicity of 1 and 4 with a multiplicity of 1.

So the image of the parabolic lens crosses the x-axis at two points:

(-8,0)

and

(4,0)

For information, I attached the graph of the function.

Hope this helps.

Do not hesitate if you need further explanation.

Thank you