Question

1. The following are the number of hours that 10 police officers have spent being trained in how to handle encounters with people who are mentally ill:

4 17 12 9 6 10 1 5 9 3

Calculate the (a) range, (b) inter-quartile range, (c) variance, and (d) standard deviation.
(Use N)

Answer 1

`Range = 16`

`Inter\ Quartile\ Range = 6.75`

`Variance = 20.44`

`Standard\ Deviation = 4.52`

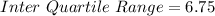
Explanation:

Given

4, 17, 12, 9, 6, 10, 1, 5, 9, 3

Calculating the range;

`Range = Highest - Lowest`

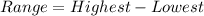
From the given data;

Highest = 17 and Lowest = 1

Hence;

`Range = 17 - 1`

`Range = 16`

Calculating the Inter-quartile Range

Inter quartile range (IQR) is calculates as thus

`IQR = Q_3 - Q_1`

Where

Q3 = Upper Quartile and Q1 = Lower Quartile

Start by arranging the data in ascending order

1, 3, 4, 5, 6, 9, 9, 10, 12, 17

N = Number of data; N = 10

---------------------------------------------------------------------------------

Calculating Q3

`Q_3 = (3)/(4)(N+1) th\ item`

Substitute 10 for N

`Q_3 = (3)/(4)(10+1) th\ item`

`Q_3 = (3)/(4)(11) th\ item`

`Q_3 = (33)/(4) th\ item`

`Q_3 = 8.25 th\ item`

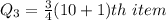
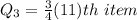
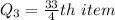
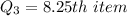
Express 8.25 as 8 + 0.25

`Q_3 = (8 + 0.25) th\ item`

`Q_3 = 8th\ item + 0.25 th\ item`

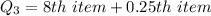
Express 0.25 as fraction

`Q_3 = 8th\ item +(1)/(4) th\ item`

`Q_3 = 8th\ item +(1)/(4) (9th\ item - 8th\ item)`

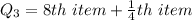
From the arranged data;

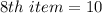`8th\ item = 10` and
`9th\ item = 12`

`Q_3 = 8th\ item +(1)/(4) (9th\ item - 8th\ item)`

`Q_3 = 10 +(1)/(4) (12 - 10)`

`Q_3 = 10 +(1)/(4) (2)`

`Q_3 = 10 +0.5`

`Q_3 = 10.5`

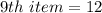
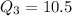
Calculating Q1

`Q_1 = (1)/(4)(N+1) th\ item`

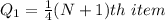
Substitute 10 for N

`Q_1 = (1)/(4)(10+1) th\ item`

`Q_1 = (1)/(4)(11) th\ item`

`Q_1 = (11)/(4) th\ item`

`Q_1 = 2.75 th\ item`

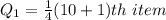
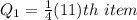
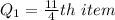
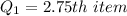
Express 2.75 as 2 + 0.75

`Q_1 = (2 + 0.75) th\ item`

`Q_1 = 2nd\ item + 0.75 th\ item`

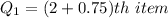
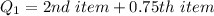
Express 0.75 as fraction

`Q_1 = 2nd\ item +(3)/(4) th\ item`

`Q_1 = 2nd\ item +(3)/(4) (3rd\ item - 2nd\ item)`

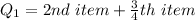
From the arranged data;

`2nd\ item = 3` and
`3rd\ item = 4`

`Q_1 = 3 +(3)/(4) (4 - 3)`

`Q_1 = 3 +(3)/(4) (1)`

`Q_1 = 3 +0.75`

`Q_1 = 3 .75`

---------------------------------------------------------------------------------

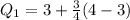
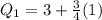
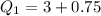
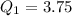
Recall that

`IQR = Q_3 - Q_1`

`IQR = 10.5 - 3.75`

`IQR = 6.75`

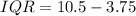
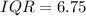
Calculating Variance

Start by calculating the mean

`Mean = (1+3+4+5+6+9+9+10+12+17)/(10)`

`Mean = (76)/(10)`

`Mean = 7.6`

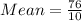
Subtract the mean from each data, then square the result

`(1 - 7.6)^2 = (-6.6)^2 = 43.56`

`(3 - 7.6)^2 = (-4.6)^2 = 21.16`

`(4 - 7.6)^2 = (-3.6)^2 = 12.96`

`(5 - 7.6)^2 = (-2.6)^2 = 6.76`

`(6 - 7.6)^2 = (-1.6)^2 = 2.56`

`(9 - 7.6)^2 = (1.4)^2 = 1.96`

`(9 - 7.6)^2 = (1.4)^2 = 1.96`

`(10 - 7.6)^2 = (2.4)^2 = 5.76`

`(12 - 7.6)^2 = (4.4)^2 = 19.36`

`(17 - 7.6)^2 = (9.4)^2 = 88.36`

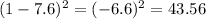
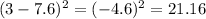
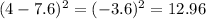
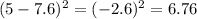
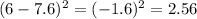
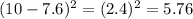
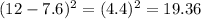
Sum the result

`43.56 + 21.16 + 12.96 + 6.76 + 2.56 + 1.96 + 1.96 + 5.76 + 19.36 + 88.36 = 204.4`

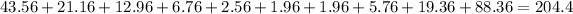
Divide by number of observation;

`Variance = (204.4)/(10)`

`Variance = 20.44`

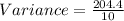
Calculating Standard Deviation (SD)

`SD = √(Variance)`

`SD = √(20.44)`

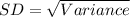
`SD = 4.52` (Approximated)