Answer:
Option (4)
Explanation:
If the given exponential function is in the form of f(x) =
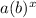
From the graph we find that two points (0, 3) and (0.5, 6) lie on the graph.
For (0, 3),
f(0) =
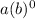
3 = a
For (0.5, 6),
f(0.5) =
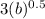
6 =
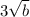
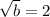
b = 4
Therefore, value of b in the given function 'f' is 4.
Option (4) will be the answer.