Answer:
Step-by-step explanation:
The rod will act as pendulum for small oscillation .
Time period of oscillation
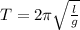
angular frequency ω = 2π / T
=
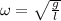
b )
ω = 20( given )
velocity = ω r = ω l
Let the maximum angular displacement in terms of degree be θ .
1/2 m v ² = mgl ( 1 - cosθ ) ,
[ l-lcosθ is loss of height . we have applied law of conservation of mechanical energy .]
.5 ( ω l )² = gl( 1 - cos θ )
.5 ω² l = g ( 1 - cosθ )
1 - cosθ = .5 ω² l /g
cosθ = 1 - .5 ω² l /g
θ can be calculated , if value of l is given .