Answer:
x = 18311.61 m
Explanation:
It is given that, An observer (O) spots a bird flying at a 55° angle from a line drawn horizontal to its nest. The distance from the observer (O) to the bird (B) is 15,000 ft. We need to find the distance between the bird and the nest. It is based on trigonometry. So,
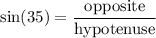
Let x is the distance between the bird and the nest
So,
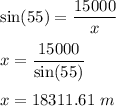
So, the distance between the bird and the nest is 18311.61 m.