Answer:
The p-value is 0.809.
Explanation:
In this case we need to perform a significance test for the standard deviation.
The hypothesis is defined as follows:
H₀: σ₀ = 4 vs. Hₐ: σ₀ ≤ 4
The information provided is:
n = 9
s = 3
Compute the Chi-square test statistic as follows:
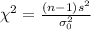
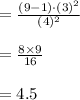
The test statistic value is 4.5.
The degrees of freedom is:
df = n - 1
= 9 - 1
= 8
Compute the p-value as follows:
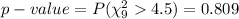
*Use a Chi-square table.
Thus, the p-value is 0.809.