Answer:
x(t) = −2 cos (
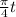 −
−
 ) + 4 cos (
) + 4 cos (
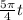 )
)
Step-by-step explanation:
Given:
Fundamental period of real valued continuous-time periodic signal x(t) = T = 8
Non-zero Fourier series coefficients for x(t) :
a₁ =
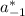 = j
= j
a₅ =
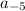 = 2
= 2
To find:
Express x(t) in the form
∞
x(t) = ∑ A
 cos ( w
cos ( w
 t + φ
t + φ
 )
)
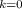
Solution:
Compute fundamental frequency of the signal:
w₀ = 2 π / T
= 2 π / 8 Since T = 8
w₀ = π / 4
∞
∑
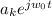
x(t) = k=⁻∞
=
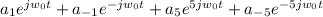
=
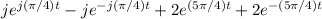
= −2 sin (
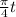 ) + 4 cos (
) + 4 cos (
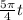 )
)
= −2 cos (
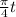 −
−
 ) + 4 cos (
) + 4 cos (
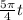 )
)