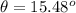Answer:
The angle is
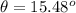
Step-by-step explanation:
From the question we are told that
The distance of the dartboard from the dart is
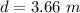
The time taken is
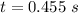
The horizontal component of the speed of the dart is mathematically represented as

where u is the the velocity at dart is lunched
so
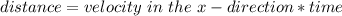
substituting values
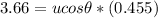
=>
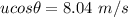
From projectile kinematics the time taken by the dart can be mathematically represented as
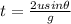
=>
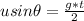
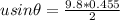

=>

![\theta = tan^(-1) [0.277]](https://img.qammunity.org/2021/formulas/physics/college/8ir28ozjkanhurrjkwqjskbenb95mywayh.png)