Question

Find the 12th term of the following geometric sequence.
10, 30, 90, 270,

Answer 1

The 12th term is 1771470

Explanation:

Since the above sequence is a geometric sequence

An nth term of a geometric sequence is given by

`A(n) = a(r)^(n - 1)`

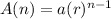
where a is the first term

r is the common ratio

n is the number of terms

From the question

a = 10

To find the common ratio divide the previous term by the next term

That's

r = 30/10 = 3 or 90/30 = 3 or 270/90 = 3

Since we are finding the 12th term

n = 12

So the 12th term is

`A(12) = 10( {3})^(12 - 1)`

`A(12) = 10 ({3})^(11)`

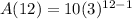
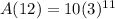
A(12) = 1771470

Hope this helps you