Answer:
B. The company should have 8 production runs each year.
Explanation:
From the given information:
A paint manufacturer has a uniform annual demand for 16,000 cans of automobile primer
It costs $4 to store one can of paint for one year
$500 to set up the plan for production of the primer
Let x be the number of cans of paint produced during each production run
Let y be the number of production runs.
If the total storage and setup cost is C = 500y + 2c
and cy = 16000
Then c = 16000/y
From;
C = 500y + 2c
Replacing c with 16000/y, we have;
C = 500y + 2(16000/y)
C = 500y + 32000/y
in order to minimize the total storage and setup costs
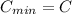
Therefore
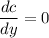
⇒ 500 - 32000/y² =0
y² = 32000/500
y² = 320/5
y² = 64
y = (√64)
y = 8
Therefore; The company should have 8 production runs each year in order to minimize the total storage and setup costs