Answer:
A)
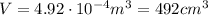
B)
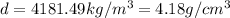
Step-by-step explanation:
A) Using the Archimedes' force we can find the weight of water displaced:
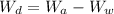
Where:
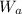 : is the weight of the block in the air = 20.1 N
: is the weight of the block in the air = 20.1 N
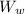 : is the weight of the block in the water = 15.3 N
: is the weight of the block in the water = 15.3 N
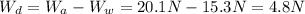
Now, the mass of the water displaced is:

The volume of the block can be found using the mass of water displaced and the density of the water:
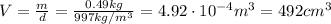
B) The density of the block can be found as follows:
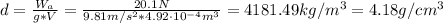
I hope it helps you!