Answer:
The answer is below
Explanation:
Use the given degree of confidence and sample data to find a confidence interval for the population standard deviation . Assume that the population has a normal distribution. Round the confidence interval limits to the same number of decimal places as the sample standard deviation.
Answer: Given that:
Sample size (n) = 14, mean (
 ) = 161.3, standard deviation (
) = 161.3, standard deviation (
 ) = 12.6
) = 12.6
Confidence(C)= 90% = 0.9
α = 1 - C = 1- 0.9 = 0.1
α/2 = 0.1 / 2 = 0.05
The z score of α/2 correspond to a z score of 0.45 (0.5 - 0.05). This gives:
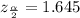
The margin of error (E) is given by the formula:

The confidence interval = μ ± E = 161.3 ± 5.5 = (155.8, 166.8)
The confidence interval is between 155.8 lb and 166.8 lb. There is a 90% confidence that the mean is between 155.8 lb and 166.8 lb.