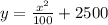Question

A satellite dish is being designed so that it can pick up radio waves coming from space. The satellite dish will be in the shape of a parabola and will be positioned above the ground such that its focus is 50 ft above the ground. Using the ground as the x-axis, where should the base of the satellite be positioned? Which equation best describes the equation of the satellite?

Answer 1

(0, 25); y = one over one hundred x2 + 25

Explanation:

If your on question 7 of (04.04 MC)

It should be the third option. (C)

Answer 2

`y=(x^2)/(100)+2500`

Explanation:

Given that the satellite is in the shape of parabola and will be positioned above the ground such that its focus is 50 ft, above ground.

let the point at the ground be (0,0) and focus (0,50). Thus, The base is at equal distance from the ground and focus that the vertex is at

(h,k) =(0,25).

Obtain the equation that describes the equation of the satellite as,

`(x-h)^2 =4a(y-k)\\</p><p>\Rightarrow (x-0)^2=4(25)(y-25)\\</p><p>\Rightarrow x^2=100(y-25)\\</p><p>\Rightarrow x^2 =100y-2500\\</p><p>\Rightarrow y=(x^2)/(100)+2500`

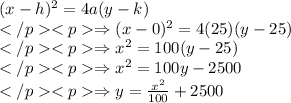
Thus, the equation of satellite is
`y=(x^2)/(100)+2500`