Answer:
Remaining amount of the element = 31.5 mg
Explanation:
Half life of radioactive Iodine is
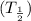 = 60 days
= 60 days
Formula to get the remaining element after t days is,
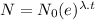
Where
 = decay constant of the radioactive element
= decay constant of the radioactive element
t = duration of the decay (in days)
 = Initial amount of the element
= Initial amount of the element
N = final amount after decay
For half life period 't' = 60 days
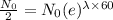
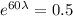
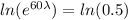
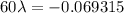
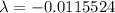
Remaining amount of the element after 40 hours,
N =
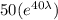
=
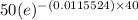
= 50(0.62996)
= 31.49
≈ 31.5 mg
Therefore, remaining amount of the element after 40 days is 31.5 mg.